[Dynamo+=Python] Surcharge des Opérateurs...géométrique

PointA + PointB = ?

Dans la logique on obtiendrait un nouveau Point (ou un nouveau vecteur) avec des coordonnées résultant de la somme des coordonnées du PointA et du PointB, mais si l'on souhaite que le résultat de l'addition retourne un type différent?

C'est là que l'utilisation de la surcharge des opérateurs Python devient intéressant.

Cette fonctionnalité en Python, qui permet à un même opérateur d’avoir une signification différente en fonction du contexte.

Voici un exemple d'utilisation  dans un contexte Dynamo

Ci-dessous une Classe où, à chaque création d'instance de celle-ci on crée un Point géométrique via des coordonnées X, Y, Z.

Et on y rajoute des surcharges d'opérateurs afin d'effectuer des opérations géométriques.

  
import sys
import clr
clr.AddReference('ProtoGeometry')
from Autodesk.DesignScript.Geometry import *
import Autodesk.DesignScript.Geometry as DS


class MyCustumGeom():
    def __init__(self, *args):
        if isinstance(args[0], (int, float)):
            self.DS_geo = DS.Point.ByCoordinates(*args)
        elif isinstance(args[0], Curve):
            self.DS_geo = args[0]       
            
    def getCurvePoint(self):
        lstCurv = self.DS_geo.Curves()
        lstPoint = [x.StartPoint for x in lstCurv]
        lstPoint.append(self.DS_geo.EndPoint)   
        return lstPoint

    def __add__(self, other):
        if isinstance(self.DS_geo, Point): 
            DSline = DS.PolyCurve.ByPoints([self.DS_geo, other.DS_geo])
            return MyCustumGeom(DSline)
            
        elif isinstance(self.DS_geo, PolyCurve):
            lstPoint = self.getCurvePoint()
            lstPoint.append(other.DS_geo)
            DSline = DS.PolyCurve.ByPoints(lstPoint)
            return MyCustumGeom(DSline)
            
        else: return "Error"    
            
    def __sub__(self, other):
        if isinstance(self.DS_geo, PolyCurve):
            lstPoint = [x for x in self.getCurvePoint() if x.DistanceTo(other.DS_geo) > 0.01]
            DSline = DS.PolyCurve.ByPoints(lstPoint)
            return MyCustumGeom(DSline)
            
        else: return "Error"    
        
    def __eq__(self, other):
        if isinstance(self.DS_geo, Point): 
            return self.DS_geo.DistanceTo(other.DS_geo) < 0.01
        return False    
        
    def __ne__(self, other):
        if isinstance(self.DS_geo, Point): 
            return self.DS_geo.DistanceTo(other.DS_geo) > 0.01
        return True     
        
    def __iadd__(self, other):
        return self.__add__(other)
        
        
    def __isub__(self, other):
        return self.__sub__(other)  
        
    __radd__ = __add__  
    
    __rsub__ = __sub__  

Nous allons découvrir quelques principaux opérateurs du langage. Ces exemples ne sont pas exhaustifs et présentent juste la méthodologie à suivre.

Pour une liste complète, je vous invite à consulter la documentation du module operator :

https://docs.python.org/2/library/operator.html

https://docs.python.org/3/library/operator.html.

Maintenant passons aux usages avec quelques exemples: 

• la Comparaison d'égalité: operator.__eq__(a, b)

Créons 2 instances de cette classe (Point géométrique) et comparons-les  ( == ).

   

Remarques:

• Bien entendu si vous avez seulement à comparer des points passer directement par la méthode : Geometry.IsAlmostEqualTo(Geometry)

• On peut également implémenter d'autres opérateurs de comparaison pour comparer les distances des coordonnées depuis l'origine avec Pythagore:

 __lt__(a, b) →   pta < ptb

__gt__(a, b) →  pta > ptb

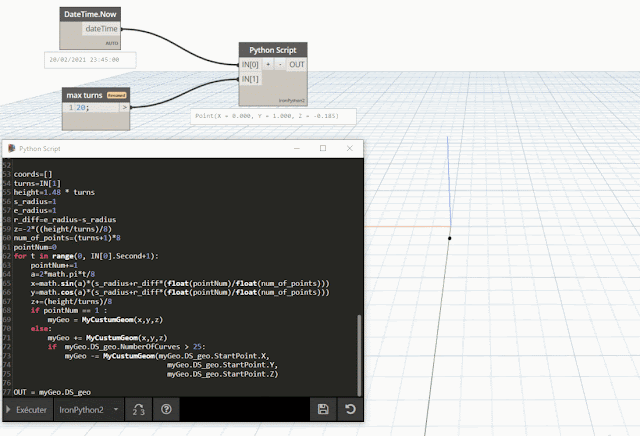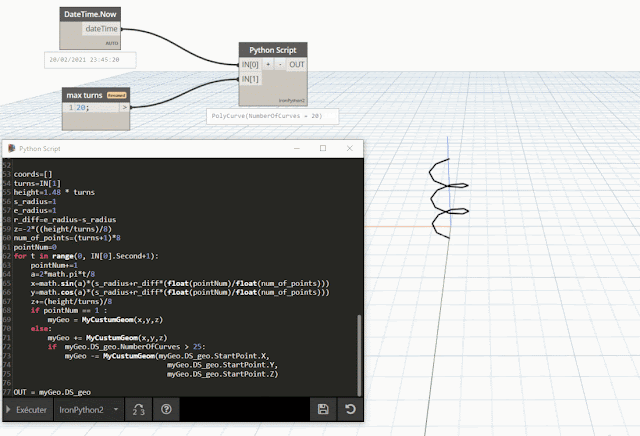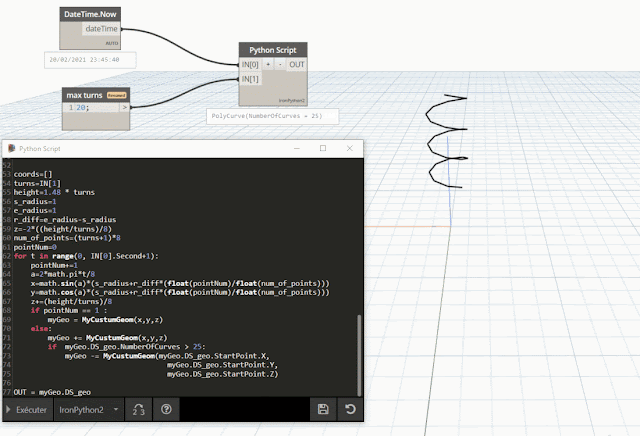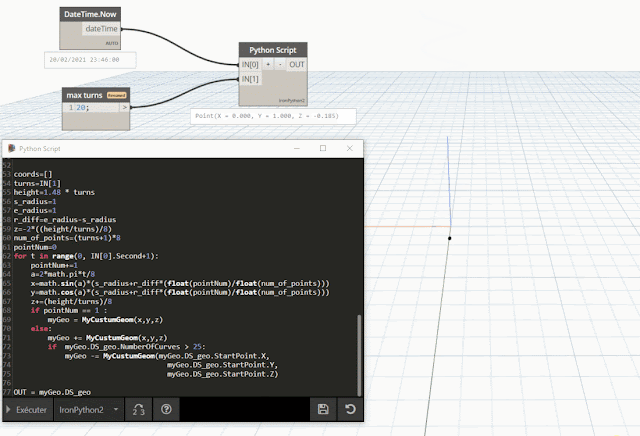
• l'ajout : operator.__add__(a, b)

ici nous allons ajouter des Points, mais plutôt que de retourner un vecteur (ou de nouvelle coordonnées), la somme de points nous retournera ici une polyligne (courbe) 

création d'une Polycurve par ajout de Points

• la soustraction : operator.__sub__(a, b)

à cette polyligne on décide finalement de retirer le deuxième point (signe - )

comparaison de courbes avant et après la soustraction d'un Point  

• l'ajout et la soustraction "In-Place": 
  operator.__iadd__(a, b)    operator.__isub__(a, b)

pour ajouter dynamiquement des points (ou des objets) une solution consiste à passer par des opérateurs d'assignement:

• += pour l'ajout de point 
• -=  pour la soustraction de point
  
  
  

Dans l'exemple ci-dessous on trace une hélice (courbe géométrique "hélix") dynamiquement de façon qu'elle ne dépasse pas 25 points, en ajoutant un point et retirant le premier point si nécessaire (à l'instar d'un deque).

Polycurve "Helix" dynamique

On retrouve également ces opérateurs d'assignement dans la souscription d'évènements (IronPython, C#, VB.Net, etc...)

En espérant que cela puisse vous donner des idées, si jamais vous décider d'écrire vos propres classes (ou librairies).