[Dynamo += Python] Opération...Vecteurs!

 

Dès lors que l'on analyse des géométries en programmation, les opérations de vecteurs deviennent vite incontournable, parmi elles le produit vectoriel et le produit scalaire.

Voici quelques particularités de ces 2 opérations avec des vecteurs unitaires

Note: vecteur unitaire = vecteur à longueur 1, appeler aussi vecteur Normalisé

• Produit scalaire de 2 vecteurs normalisés :

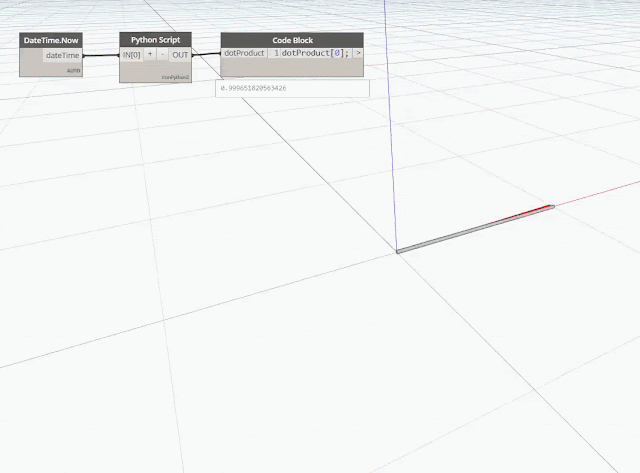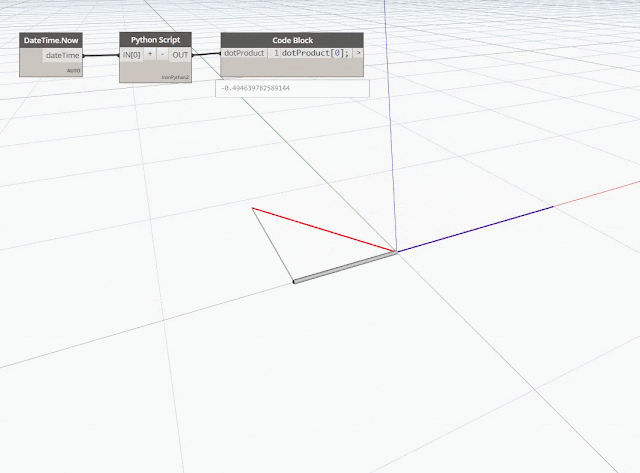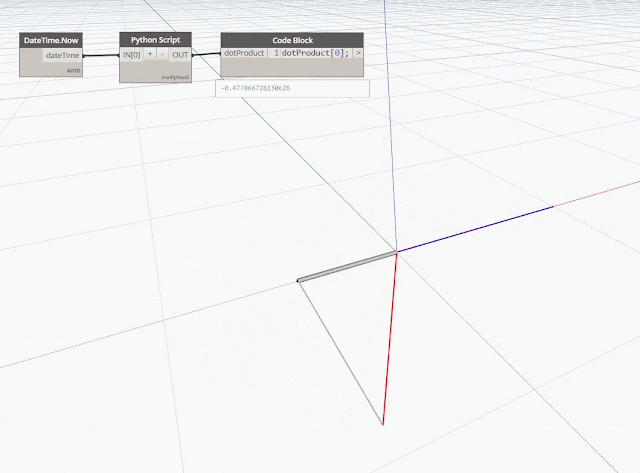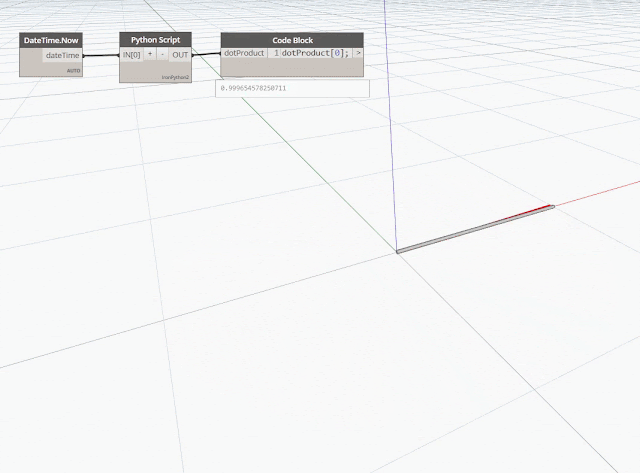
Soit le scalaire n résultant de l'opération sur un plan XY, suivant les résultats on peut en déduire que :

si n égale à -1 → les 2 vecteurs sont alignés dans le sens opposé (angle 180°)

 si n égale à 1 → les 2 vecteurs sont alignés dans le même sens (angle 0°)

si n égale à  0 → les 2 vecteurs sont perpendiculaires (angle 90°)

Note:
v1 et v2 étant normaux le résultat varie entre -1 et 1:

• Produit vectoriel de 2 vecteurs (normalisés ou non) :

Soit le vecteur résultant de l'opération sur un plan XY, suivant les résultats de la base directe, on peut en déduire que :

si la composante Z du vecteur>  0 → l'angle formé entre u et vers v est positif

si la composante Z du vecteur<  0 → l'angle formé entre u et vers v est négatif

si la longueur du vecteur=  0 →  u et v sont parallèles (colinéaires)    

Quelques exemples d'applications

• Avec le produit scalaire (dot Product) :

• obtenir la distance entre 2 faces parallèles
  

def compute_distance_planarfaces(faceA, faceB):
	bbxUVa = faceA.GetBoundingBox()
	pta = faceA.Evaluate((bbxUVa.Min + bbxUVa.Max) / 2.0)
	normalA = faceA.FaceNormal #or faceA.ComputeNormal((bbxUVa.Min + bbxUVa.Max) / 2.0)
	#
	bbxUVb = faceB.GetBoundingBox()
	ptb = faceB.Evaluate((bbxUVb.Min + bbxUVb.Max) / 2.0)
	if pta.DistanceTo(ptb) < 0.001:
		return 0.0
	vector_between_faces = ptb - pta 
	# Project this vector onto the normal to get the distance
	distance = vector_between_faces.DotProduct(normalA.Normalize())
	return abs(distance)

• vérifier si 2 vecteurs sont perpendiculaires

def isPerpendicular(v1, v2):
    #with Revit API
    return v1.DotProduct(v2) == 0

• Ordonner une liste de points suivant un vecteur

On utilise ici la similarité cosinus.
La similarité cosinus donne la similarité de deux vecteurs à n dimensions en déterminant le cosinus de leur angle.

def cosine_similarity(point, vector):
    dot_prod = point.DotProduct(vector)
    mag_point = point.GetLength()
    mag_vector = vector.GetLength()
    # avoid division by zero if the magnitude is zero
    if mag_point == 0 or mag_vector == 0:
        return 0
    return dot_prod / (mag_point * mag_vector)

import random
import numpy as np
# generate 2D array of shape (30, 2) with random integers
random_2D = np.random.randint(0, 30, (30,2))
lst_points = [XYZ(x, y, 0) for x, y in random_2D]
# 
vector_direction = XYZ(2, 5, 0)
sorted_points = sorted(lst_points, key=lambda p: cosine_similarity(p, vector_direction))




• trouver l'orientation d'une face par rapport aux points cardinaux

import sys
import clr
clr.AddReference('ProtoGeometry')
from Autodesk.DesignScript.Geometry import *

clr.AddReference('RevitAPI')
import Autodesk
from Autodesk.Revit.DB import *

clr.AddReference('RevitServices')
from RevitServices.Persistence import DocumentManager
doc = DocumentManager.Instance.CurrentDBDocument

clr.AddReference('RevitNodes')
import Revit
clr.ImportExtensions(Revit.Elements)
clr.ImportExtensions(Revit.GeometryConversion)


def getOrientation(vecTrueNorth, vecTrueEast, solidFace):
    #with Revit API
    faceNorm = solidFace.FaceNormal
    dotP_N = faceNorm.DotProduct(vecTrueNorth)
    dotP_E = faceNorm.DotProduct(vecTrueEast)
    #0.7 = Pi / 4 or (45°)
    if  dotP_N > 0.7 and abs(dotP_E) <= 0.7:
        return "North"
    elif dotP_N < -0.7 and abs(dotP_E) <= 0.7:
        return "South"
    elif dotP_E > 0.7 and abs(dotP_N) <= 0.7:
        return "East"       
    elif dotP_E < -0.7 and abs(dotP_N) <= 0.7:
        return "West"
    else:
        return None
        
room = UnwrapElement(IN[0])

currentLocation = doc.ActiveProjectLocation
origin = XYZ(0, 0, 0)
projectPosition = currentLocation.GetProjectPosition(origin)
angleToNorth = projectPosition.Angle
vecNorth = XYZ.BasisY 
vecEast = XYZ.BasisX 
rotTransf = Transform.CreateRotation(XYZ.BasisZ,  - angleToNorth)
vecTrueNorth = rotTransf.OfVector(vecNorth)
vecTrueEast = rotTransf.OfVector(vecEast)

calculator = SpatialElementGeometryCalculator(doc)
resultOrient = list()

if calculator.CanCalculateGeometry(room):
    results = calculator.CalculateSpatialElementGeometry(room)
    roomSolid = results.GetGeometry()
    roomMaterial = list()
    for face in roomSolid.Faces:
        for subface in results.GetBoundaryFaceInfo(face):
            if subface.SubfaceType == SubfaceType.Side:     
                boundingElement = subface.GetBoundingElementFace()
                lnkelemId = subface.SpatialBoundaryElement 
                materialId = boundingElement.MaterialElementId  
                elem = doc.GetElement(lnkelemId.HostElementId )
                surfaceDs = face.ToProtoType()
                nameOrient = getOrientation(vecTrueNorth, vecTrueEast, face)
                resultOrient.append([surfaceDs[0], elem, nameOrient])

OUT =  resultOrient

• Avec le produit vectoriel (cross product) 

• vérifier si 2 vecteurs sont parallèles

def isParallel(v1, v2):
    return v1.CrossProduct(v2).IsAlmostEqualTo(XYZ(0, 0, 0))

• vérifier si un arc est dans le sens horaire

def isClockwise(arc):
    #with Dynamo API
    pStart = arc.StartPoint
    pCenter = arc.CenterPoint
    pEnd = arc.EndPoint
    vecta = Vector.ByTwoPoints(pCenter, pStart)
    vectb = Vector.ByTwoPoints(pCenter, pEnd)
    cp = vecta.Cross(vectb)
    return cp.Z < 0  

• ou encore pour vérifier si un point est situé dans un polygone

import sys
import clr
clr.AddReference('ProtoGeometry')
from Autodesk.DesignScript.Geometry import *
polygon = IN[0]
pointCheck = IN[1]

def isInsidePolyg(polygon, pointCheck):
    #with Dynamo API
    lstangle =[]
    pointPolyg = polygon.Points
    for idx, pt in enumerate(pointPolyg):
        if idx > 0:
            vecta = Vector.ByTwoPoints(pointCheck, pointPolyg[idx -1])
            vectb = Vector.ByTwoPoints(pointCheck, pt)
            cross = vecta.Cross(vectb).Normalized()
            angle = vecta.AngleWithVector(vectb)
            vecta.Dispose()
            vectb.Dispose()
            cross.Dispose()
            lstangle.append(angle * cross.Z)

    return abs(sum(lstangle)) > 180 

OUT = isInsidePolyg(polygon, pointCheck)